Various Projects in Computer Animation
 |
Course: CS 274C - Computer Animation |
Course Description
Introduction to computer animation, including basic principles of character modeling, forward and inverse kinematics, forward and inverse dynamics, motion capture animation techniques, physics-based animation of particles and systems, and motor control.
Movie Quick Links (more details below)
Hermite Splines |
Particle System |
|
Particle systems are another popular technique in computer animation. They are simple to implement and useful for modeling natural phenomena with many degrees of freedom such as fluids, fire, explosions, etc. In this project, we build a system of particles (shown in green) connected by several springs (white lines). We create a dynamic simulation, meaning that physical forces are present and drive the particles motion. In particular, we add gravity to the simulation, spring forces with damping to retain the systems shape, and a ground penalty force that "pushes up" on the cube as it hits the ground. In this example, the particle system exhibits "jello" like behavior as it bounces on the ground. For each particle, we must use an integration method to compute the particle positions at each time step from their accelerations due to forces. In this project we use Forward Euler Integration, Symplectic Euler Integration, and Verlet Integration. These methods differ in simplicity (computational speed) and simulation stability (numerical fidelity and prevention of crashes) which usually conflict. The movies below use the Verlet Integration method. The left movie shows the particle system bouncing on
the ground. |
 (click to watch movie) |
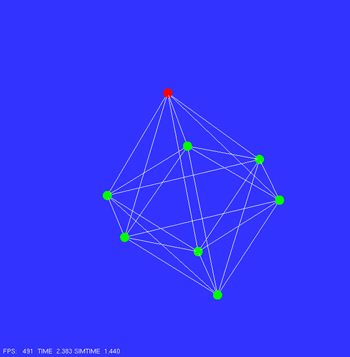 (click to watch movie) |
Inverse Kinematics |