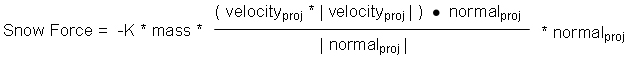Snowboarding Simulation in a Physics-based Environment
 |
Course: CS 269 -
Current Topics in Artificial Intelligence: Artificial Life for Computer Graphics
and Vision |
Course Description
Investigation of the important role that concepts from artificial life--an emerging discipline that spans computational and biological sciences--that plays in the construction of advanced computer graphics and vision models for virtual reality, animation, interactive games, active vision, visual sensor networks, medical image analysis, etc. Focus on comprehensive models that realistically emulate variety of living things--plants and animals--from lower animals to humans. Students exposed to effective computational modeling of natural phenomena of life and their incorporation into sophisticated, self-animating graphical entities. Topics include modeling plants using L-systems, biomechanical simulation and control, behavioral animation, reinforcement and neural-network learning of locomotion, cognitive modeling, artificial animals and humans, human facial animation, and artificial evolution.
Project Overview
The goal of the project was to build a snowboarding simulation based in a physical environment with forces, as well as the design of a dynamic controller for such a motion. It was envisioned that exploring the details of the snowboarding motion might reveal a mathematical model for joint configurations that could capture the cyclic behavior.
Snowboarding, along with all other board sports such as skateboarding and surfing, is a complex motion and is difficult to learn for humans. On average, I have observed that it takes one nearly five full days to properly learn the entire carving motion. This reason made the project both challenging and interesting.
The results of the project include successfully developing a model and environment for a physical snowboarding simulation that was verified by a key-framed motion scenario. A basic dynamic controller was also developed to handle arbitrary turns of the character while maintaining balance in the environment. Many of the key concepts of the carving motion were discovered and incorporated into the controller. It should be noted that the dynamic controller for this project was hand designed to operate for this particular character and environment. A more useful (and greatly more complex!) algorithm would act as a "black box" to train any character in any environment, to generate a dynamic controller for snowboarding.
The project was implemented in C++ and OpenGL, using the DANCE software package and the Open Dynamic Engine (ODE) for physical simulation.
Movie Quick Links (more details below)
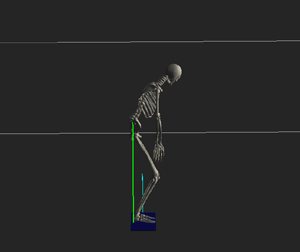
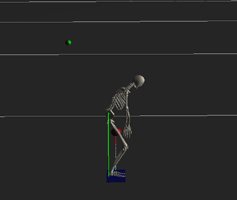
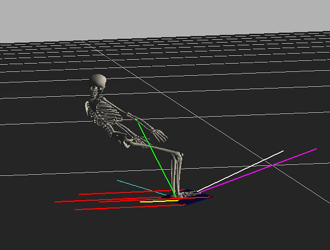
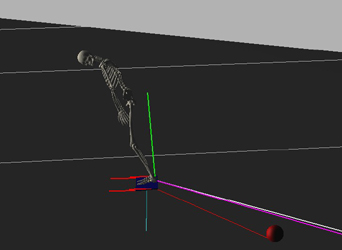
Image / Video Color Key:
4 Red Vectors – Simulated snow force on the board
Green Vector – Normal of the board
Yellow Vector – Normal's vertical projection on the slope
Cyan Vector – Heading of the board
Purple Vector – Board velocity's vertical projection on the slope
White Vector – Character velocity's vertical projection on the slope
Red ball – Current marker with a red line to it (or orange if the character is
balanced)
Green ball –
Non-current marker
Model |
|
The DANCE software package provides a skeleton character with realistic human joints. The skeleton articulated object was attached to a snowboard (flat and long rigid body) by a total of 4 stiff zero-length springs, located at the toes and heels of each foot. This is consistent with the real bindings of a snowboard that consist of two small straps which lock in the snow boots. The snowboard was roughly 7% of the mass of the skeleton. The character was only given 8 controllable degrees of freedom. To be consistent with the restricted ankle movement of the boots and bindings, proper joint limits were enforced. The following table shows the relevant joints and their limitations. |
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
All other joints that do not appear in this table were given the default joint limits from the skeleton topology. It can be noted that the ankles are severely restricted, disallowing backward rotation and twist. An important observation is that the entire snowboarding motion can be achieved mostly through x-axis joint rotations (bend) of the legs and trunk, along with a slight twist of the trunk. This seems reasonable, as real snowboarding requires primarily leaning motions. |
 (click image to enlarge) |
 (click image to enlarge) |
Environment |
|
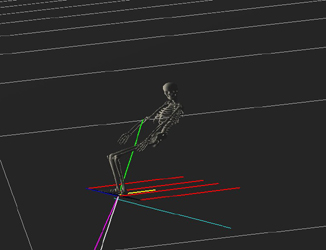
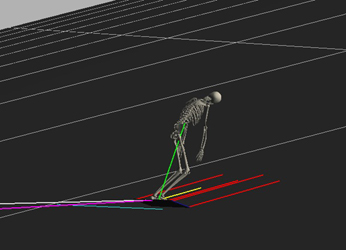
An inclined plane was added at 20 degrees, with minimal friction. Conveniently, ODE already supplies collision support between all rigid bodies in the scene (namely between the ground and the snowboard). The skeleton was initialized at rest on the slope and a gravity force was added. A following snow force was added to simulate the effects of the snow on the board for both deceleration and turning. It is based on centripetal force and was designed to account for board orientation versus board velocity.
where K is a constant and the mass includes both the skeleton and snowboard. The velocity projection is the board’s velocity vector projected vertically onto the slope. The normal projection is the board’s unit normal vector projected onto the slope. The snow force is applied to the four corners of the snowboard (each corner applying 25% of the total force). The resulting snow force vector is always pointing in the direction of the board’s normal projection. Therefore, the snow force is always decelerating or turning the board’s movement, but never lifting upward on it. The forces of gravity naturally pull the board down the slope, and the combination of the two forces create the carving motion. As the board increases its vertical angle with the slope (more lean), so does the magnitude of the snow force as more snow pushes against it. Similarly, the more the board is angled (opposing) the velocity of the board, the larger the force. The snow force is zero when the board is completely on the slope or the board has exceeded a threshold angle with that of the slope. |
 (click image to enlarge) |
 (click image to enlarge) |
Key-frame Sequence |
|
The model and environment were tested by using a key-frame engine to generate a physically plausible snowboarding animation. Key-framing is a popular animation technique where an animator supplies a few major or "key" frames for the animation, while a program interpolates all the frames that come in between these key frames. In particular, this key-frame engine sets the necessary joint torques for each key frame or "pose" the character must match down the slope. A full 3 turn carving motion was hand constructed using 35 key-frames. The key-frame construction allowed for two important discoveries: it revealed the relevant degrees of freedom in the motion and the basic locomotion strategies to help design the dynamic controller (to be explained). Since the character begins the simulation at rest, the locomotion strategy actually differs at high velocities versus low velocities. At first, the character must laboriously shift its weight to turn the board and lean dramatically to leverage the snow force. Once velocity increases, the character can simply use various leg configurations and leaning motions to achieve the toe-side and heel-side turns. Some important properties of the motion were discovered. For one, the character’s center of mass should always be directly in line with the board’s normal during turns for proper balance. Also, trunk twist also plays a key role in turns, used for both stability and helping the twist of the hip. As a general rule, right turns require the front leg to be more bent than the back, and left turns require the back leg to be more bent than the front. This is not always the case however, as some turns require only a lean to use the board’s natural inclination to face downward. Below is the movie of the key-frame sequence. At first, the character must shift its weight and lean dramatically to leverage the snow force for the initial turn. The first left turn is taken by leaning and bending the right leg more. As the right turn is taken, the character leans far down for a very sharp turn (and builds up a lot of speed!). To recover from this sharp turn, a series of balance corrections are performed to keep the character from sliding out. A final sequence of braking occurs as the character leans far back to counter the large snow force. |
Dynamic Controller |
|
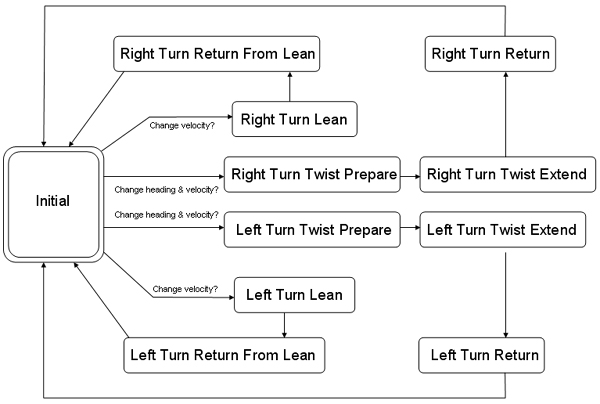
The final stage of the project was to develop a dynamic proportional-integral-derivative controller (sometimes called a PID or PD controller) that uses spring joint torques and damping to continuously update the proper joint angles for the snowboarding motion. It was the goal to have various sequential markers placed along the slope which would attract the character and therefore influence the path traveled. This was preferred over exact path matching (i.e. splines) because real snowboarding is rarely performed in this way. The controller uses the following useful angles in the algorithm. These angles are normalized between -1 and +1. - Heading angle: Angle
between board heading and target vector (from current position to target)
The basic strategy of the controller is to align both the heading and velocity of the board towards the current target (bring the heading and velocity angles to 0). It is also important to continuously monitor the balance angle for adjustments that keep the angle as close to 0 as possible. The best results were achieved using a state machine (shown below) of general strategies rather than an approach using direct interpolations of generic poses of some sort. Most states typically generate desired joint angles when entered and carry out updates towards these angles in specific fixed increments. This ensures smooth motion and provides simulation stability. |
 |
|
At the initial stage, the controller begins by evaluating the balance angle to make sure the character is roughly balanced within a threshold (more below). When balanced, it evaluates the heading and velocity angles and determines whether a combined twist and turn (heading and velocity update) or a simple lean (velocity update) is required. The turn direction (left or right) is also determined by the velocity angle. The heading angle is offset slightly to encourage overshooting the target vector, since the board naturally wants to return to point down the slope. |
Maintaining Balance |
|
The balance mechanism of the dynamic controller will continuously run at every step unless explicitly disabled by the current state. The mechanism evaluates the current balance angle, which will be non zero if the character is not balanced (character’s velocity does not match the board’s velocity). The magnitude of the velocities is currently ignored but could have represented the imbalance due to side leaning of the body. All balance adjustments are made to the legs. Trunk adjustments did not necessarily have to be excluded, but this helped to simplify the algorithm. When the character is bent too far forward, it will respond by bending the knees and thighs more and the ankles less to bring the trunk back. Conversely, when the character is bent too far back it will bend the knees and thighs less and the ankles more. The following formula will calculate the angle step delta of the joints: Step size = K * balance_angle^2 * |board_velocity| where K is a step constant. The balance angle is squared to produce larger adjustments for higher imbalance. Also as board velocity increases, the forces become stronger and require larger adjustments. Twice the step size is used for the knees. Below is a movie demonstrating the balance mechanism. The character is instructed to lean its trunk forward, ordinarily tumbling the character onto the slope. The balance mechanism automatically counters this by bending the knees and thighs more and the ankles less. As the character falls backward, the legs respond again to balance the character. |
Movies of Dynamic Controller |
|
Below are movies demonstrating turns using the dynamic controller. Again, it was the goal to have various sequential markers placed along the slope which would attract the character and therefore influence the path traveled, not necessarily requiring the character to reach the targets. Left Turn To reach the marker on the left, the character first makes a quick twist turn, but then makes another as it realizes the heading is not turned quite enough. It then leans back for snow force, but then corrects itself as the snow force quota is exceeded. |
|
Small Right Turn This scenario requires the character to turn a small amount to the right. Since the angle is small, the character makes a series of very quick twists to keep the heading and velocity correct. Once the character picks up speed (and the velocity angle diverges), the character leans forward to use snow force for the final stretch. |
|
Large Right Turn This scenario requires a very large right turn. The character begins with a very large twist to align the heading correctly. It then leans for snow force, more so than in the previous examples. Since the marker is too far away, it will not actually reach it, but the marker has successfully attracted the character and altered its path of motion. |