3-D Tetrahedral Mesh Generator for Complex Surfaces
 |
Course: Math 285J - Scientific
Computing for the Visual Effects Industry |
Course Description
The visual effects industry has been working for decades to develop technology that allows filmmakers to generate scenes that would be too dangerous, too expensive or impossible to create in real life. As time goes by the bar is being set increasingly high for the realism and complexity of such effects. One of the most challenging aspects of modern special effects is reliably reproducing the dynamics of natural phenomena such as crashing waves, smoke and fire filled explosions, swaying and colliding cloth and hair on virtual creatures as well as the interactions between these different types of phenomena. This type of dynamic behavior is very difficult to realistically reproduce without considering the underlying physical equations of motion. Though the effects industry is only concerned with generating visually plausible (as opposed to physically accurate) motion and as such it is tempting to consider a more simplified approach to creating the effect, it turns out that ignoring the physical equations results in motions that appear wrong and synthetic to the viewer. Fortunately, applied mathematicians and physicists have worked for centuries to derive equations that describe the motion of these natural phenomena. With modern scientific computing, we can solve these equations even in the presence of complex three dimensional geometric scenes. This course gives a practical introduction to the use of numerical simulation for animating such phenomena. Topics covered will include the modeling and dynamics of particle systems and rigid bodies ( e.g. stacking and falling objects in explosions/fracture), review of basic numerical methods for relevant differential equations, simulation of deformable surfaces and volumes ( e.g. cloth, skin, hair and flesh), collision detection, modeling energy functions and hard constraints and CFD for smoke, fire and water.
Project Overview
The goal of this project was to implement the Isosurface Stuffing Algorithm which constructs a 3-D tetrahedral mesh from a given surface. A tetrahedron is like a pyramid, except with a triangular base (i.e. polyhedron composed of four triangular faces).
The algorithm is fast and provides three mathematical guarantees: the tetrahedra have good dihedral angles, the boundary of the mesh is close to the surface, and provided the surface is a smooth manifold with bounded curvature and the mesh resolution is fine enough, the mesh boundary is homeomorphic to the zero-surface. These mathematical properties make the generated meshes suitable for physical simulation that undergo large deformations (e.g. fluids).
The algorithm comes in two parts: one that builds a mesh of uniform-sized tetrahedra and another that extends this algorithm by “grading” the tetrahedra, creating larger tetrahedra in the center of the mesh while keeping the surface resolution fine and uniform. This project implements both parts of the algorithm in C++ and OpenGL.
References
1. Labelle, F., Shewchuk, J., “Isosurface Stuffing: Fast Tetrahedral Meshes with Good Dihedral Angles”, ACM Transactions on Graphics, 26 (3), 2007.
|
Uniform Tetrahedra Algorithm |
|
The algorithm takes as input a surface defined by a level set of a signed distance function. In other words, we use a function that maps a 3D point in space to a signed distance to its closest point on the surface (positive inside the surface, negative outside the surface, and zero on the surface). In this sense, the surface is called an isosurface since it is defined by all the 3D points that return a constant value, namely 0. An interesting observation is that the closest point from any point to the surface is always in the direction perpendicular to the surface. 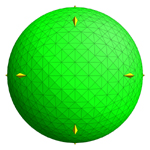Shown is a sphere level set, the easiest surface to test with since it is conveniently defined as a constant distance from its center. |
 (click image to enlarge) |
|
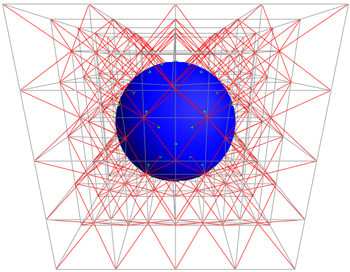
A body centered cubic (BCC) lattice is constructed about the surface. This special lattice structure produces tetrahedra with desirable angles and edge lengths. It is essentially two point grids - a Cartesian grid and a half-shifted Cartesian grid - connected by diagonals that adjoin pairs of adjacent horizontal and vertical grid edges. The algorithm first selects a subset of lattice vertices that are either inside the surface or are connected by an edge to a vertex in the surface. Next, iterative bisection is used to compute approximate intersection points (called "cut" points) where edges intersect the surface (shown in green). In the event that a cut point is too close to a lattice point, the lattice point is warped to the cut point and the cut point is discarded. The paper contains a table with different distance percentages for determining if a cut point is “too close” to a lattice point. Each distance percentage is useful for specific angle guarantees of the output mesh (such as minimum dihedral angle, max exposed plane angle, etc.). I chose the percentages to guarantee a good dihedral angle lower bound. |
 (click image to enlarge) |
|
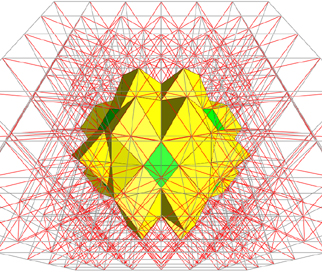
Shown are all the BCC tetrahedra
that are either completely or partially inside the surface. A BCC
tetrahedra is constructed from a horizontal edge from one grid, a vertical
edge from the other grid, and the diagonals that adjoin them.
The yellow triangle faces are those
partially inside/outside the surface and the green triangle faces are those
on the surface (due to the warping from the previous step). Note the
resolution of this grid is coarse for illustrative purposes. |
 (click image to enlarge) |
|
Each BCC lattice tetrahedron above is “stuffed” with other tetrahedra from pre-computed stencils. Each stencil contributes one to three tetrahedra to the output mesh. There are 12 different stencils for different scenarios of BCC tetrahedra, taking into account vertex sign (+, -, 0) and long vs. short lattice edge length. Each stencil may be rotated or reflected to fit a BCC tetrahedron, thereby reducing the distinct cases from 81 to 12. A few stencils are subject to a Parity Rule that helps to break symmetrical cases where a quadrilateral face must be split arbitrarily via a diagonal. Shown is the progression as we gradually apply all 12 stencils. |
     (click image to enlarge) |
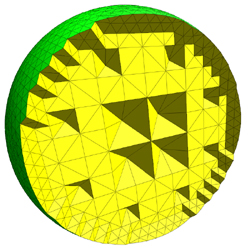
The result is a tetrahedral mesh completely filled with uniform sized tetrahedra. The right shows a cutaway view of this mesh. This mesh would not be suitable for physical simulation as it would be wasteful to process every small triangle in the center of the mesh. The next part of the algorithm is an improvement to create larger tetrahedra in the center where detail is less critical. |
  (click image to enlarge) |
|
Graded Tetrahedra Algorithm |
|
The algorithm takes as input the approximate width of tetrahedra in the output mesh, which translates to the width of surface cubes. Starting from a cube known to be on the surface, we use depth first search over the space of cubes to find all cubes that intersect the surface. We use a hash table of cubes keyed on their 3D coordinates to optimize the search.
Additional cubes are added to this set according to the Continuation Condition. This will add cubes that are adjacent to cube faces and corner vertices that intersect the surface, guaranteeing that only BCC tetrahedra will intersect the surface. |
 (click image to enlarge) |
Next we build an octree from the surface cubes. An octree is a
commonly used tree structure in graphics where 3D space is partitioned by continuously
subdividing an octant (cube) into eight child octants.
The octree is constructed from the surface cubes
which become the leaf octants of the tree, and their ancestors (shown in magenta). The octree
is kept sparse by allowing a parent octant to have any subset of its eight
children. |
 (click image to enlarge) |
In order to keep high element quality of the mesh, we enforce the Weak Balance Condition. This will create more octants in the tree where a pair of parent/child octants or adjacent octants differ in size by more than a factor of two. |
 (click image to enlarge) |
|
We convert the balanced octree to a background grid, shown to the right. This grid is comprised of BCC tetrahedra and three new types of tetrahedra: bisected BCC tetrahedra, quadrisected BCC tetrahedra, and half pyramid tetrahedra. These new types support the bridging of octants that differ by a factor of two. The primary goal is to ensure that only BCC tetrahedra intersect the surface so they can be stuffed by the stencils from the uniform algorithm. |
 (click image to enlarge) |
|
The final stage is nearly identical to the uniform tetrahedra algorithm. We compute cut points and warp the background grid just as we did for the BCC lattice. BCC tetrahedra that are either completely or partially inside the surface are “stuffed” with the stencils from the uniform algorithm. Tetrahedra of the other three types are added directly to the final mesh. Shown is the graded tetrahedral mesh and cutaway views. Notice the size of the tetrahedra gradually increase towards the center of the mesh. This mesh generated in 518 milliseconds and contains 38,952 tetrahedra on a Sony Vaio laptop with a 2.0 GHZ Intel Core 2 Duo (T7200). |
      (click image to enlarge) |
|
Additional Mesh Example |
|
Shown is another example mesh (with cutaway views) using a level set function that defines a Buddha surface. The mesh was generated in 4.603 seconds and contains 167,237 tetrahedra, with surface tetrahedra size roughly at 1% of the total surface size. All meshes were generated on a Sony Vaio laptop with a 2.0 GHZ Intel Core 2 Duo (T7200). |
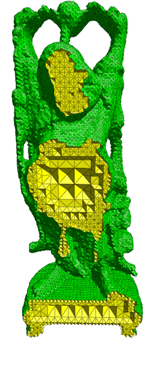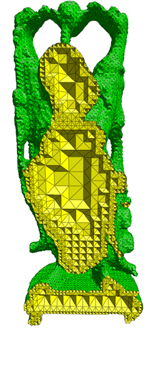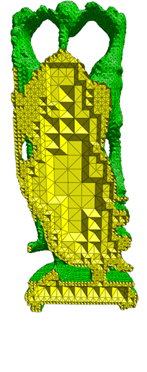
     (click image to enlarge) |
Shown are close up views of the Buddha's head at different mesh resolutions. Note the mesh was only generated for the visible region. First mesh generated in
710 milliseconds, contains 27,950 tetrahedra, with tetrahedra size at 6.7%. |
    (click image to enlarge) |
